Как стирать в машине тьюринга

Алан Тьюринг
Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A={a1, a2, a3, …, an} — внешний алфавит, служит для записи исходных данных
Q={q1, q2, q3,…, qm} — внутренний алфавит, описывает набор состояний считывающе-печатного устройства.

Машина Тьюринга
Каждая ячейка ленты может содержать символ из внешнего алфавита A = {a0,a1,…,an} (В нашем случае A={0, 1})
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = {q0,q1,…,qm}. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «<» (влево) или «.» (на месте)
· новое состояние автомата

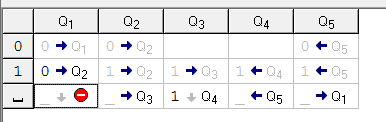
В приведенной выше таблице алфавит A ={0, 1, _} (содержит 3 символа), а внутренний алфавит Q={q1, q2, q3, q4, q0}, q0 — состояние, заставляющее каретку остановиться.
Рассмотрим несколько задач решением. Скачать машину Тьюринга Вы можете на сайте в разделе СКАЧАТЬ.
Задача 1. Пусть A={0, 1, _}. На ленте в ячейках находятся символы из алфавита в следующем порядке 0011011. каретка находится над первым символом. Необходимо составить программу, которая заменит 0 на 1, 1 на 0 и вернет каретку в первоначальное положение.
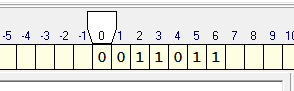
Теперь определимся с состояниями каретки. Я называю их — «желания каретки что-то сделать».
q1) Каретка должна пойти вправо: если видит 0 меняет его на 1 и остается в состоянии q1, если видит 1 — меняет его на 0 и остается в состоянии q1, если видит _ — ворачивается назад на 1 ячейку «желает что-то другое», т.е переходит в состояние q2. Запишем наши рассуждения в таблицу исполнителя. Синтаксис смотрите в справке к программе)
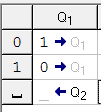
q2) Теперь опишем «желание каретки» q2. Мы должны вернуться в первоначальное положение. Для этого: если видим 1 оставляем ее и остаемся в состоянии q2 (с тем же желанием дойти до конца ряда символов); если видим 0 — оставляем его и продолжаем двигаться влево в состоянии q2; видим _ — сдвигается вправо на 1 ячейку. Вот вы оказались там, где требуется в условии задачи. переходим в состояние q0.
Посмотреть работу программы можно на видео:
Задача 2. Дано: конечная последовательность 0 и 1 (001101011101). Необходимо выписать их после данной последовательности, через пустую ячейку, а в данной последовательности заменить их на 0. Например:
Из 001101011101 получим 000000000000 1111111.
Как видите, семь единиц записались после данной последовательности, а на их местах стоят нолики.
Приступим к рассуждениям. Определим, какие состояния необходимы каретке и сколько.
q1) увидел 1 — исправь на нолик и перейди в другое состояние q2 (новое состояние вводится, чтобы каретка не поменяла на нули все единицы за один проход)
q2) ничего не менять, двигаться к концу последовательности
q3) как только каретка увидела пустую ячейку, она делает шаг вправо и рисует единичку, если она видит единичку — то движется дальше, чтобы подписать символ в конце. Как только нарисовал единицу, переходим в состояние q4
q4) проходим по написанным единицам, ничего не меняя. Как только доходим до пустой ячейки, разделяющей последовательность от единиц, переходим с новое состояние q5
q5) в этом состоянии идем начало последовательности, ничего не меняя. Доходим до пустой ячейки, разворачиваемся и переходим в состояние q1
Состояние q0 каретка примет в том случае, когда она пройдет в состоянии q1 до конца данной последовательности и встретит пустую ячейку.
Получим такую программу:

Работу Машины Тьюринга можете посмотреть на видео ниже.
Источник
Машина Тьюринга – одно из самых интригующих и захватывающих интеллектуальных открытий 20-го века. Это простая и полезная абстрактная модель вычислений (компьютерных и цифровых), которая является достаточно общей для воплощения любой компьютерной задачи. Благодаря простому описанию и проведению математического анализа она образует фундамент теоретической информатики. Это исследование привело к более глубокому познанию цифровых компьютеров и исчислений, включая понимание того, что существуют некоторые вычислительные проблемы, не решаемые на общих пользовательских ЭВМ.

Что это и кто создал
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье “О вычислимых числах с приложением к проблеме разрешимости”, которая появилась в Трудах Лондонского математического общества.

Машина Тьюринга является вычислительным устройством, состоящим из головки чтения/записи (или «сканера») с бумажной лентой, проходящей через него. Лента разделена на квадраты, каждый из которых несет одиночный символ – “0” или “1”. Назначение механизма состоит в том, что он выступает и как средство для входа и выхода, и как рабочая память для хранения результатов промежуточных этапов вычислений.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
- Неограниченная лента. Она является бесконечной в обе стороны и разделена на ячейки.
- Автомат – управляемая программа, головка-сканер для считывания и записи данных. Она может находиться в каждый момент в одном из множества состояний.
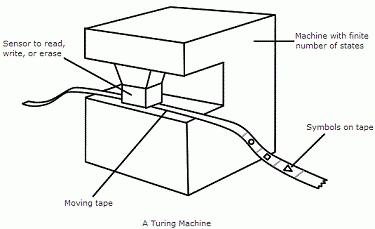
Каждая машина связывает два конечных ряда данных: алфавит входящих символов A = {a0, a1, …, am} и алфавит состояний Q = {q0, q1, …, qp}. Состояние q0 называют пассивным. Считается, что устройство заканчивает свою работу, когда попадает именно на него. Состояние q1 называют начальным – машина начинает свои вычисления, находясь на старте в нем. Входное слово располагается на ленте по одной букве подряд в каждой позиции. С обеих сторон от него располагаются только пустые ячейки.
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.

Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
- Дискретность. Цифровая машина переходит к следующему шагу n+1 только после того, как будет выполнен предыдущий. Каждый выполненный этап назначает, каким будет n+1.
- Понятность. Устройство выполняет только одно действие для одной же ячейки. Оно вписывает символ из алфавита и делает одно движение: влево или вправо.
- Детерминированность. Каждой позиции в механизме соответствует единственный вариант выполнения заданной схемы, и на каждом этапе действия и последовательность их выполнения однозначны.
- Результативность. Точный результат для каждого этапа определяет машина Тьюринга. Программа выполняет алгоритм и за конечное число шагов переходит в состояние q0.
- Массовость. Каждое устройство определено над допустимыми словами, входящими в алфавит.
Функции машины Тьюринга
В решении алгоритмов часто требуется реализация функции. В зависимости от возможности написания цепочки для вычисления, функцию называют алгоритмически разрешимой или неразрешимой. В качестве множества натуральных или рациональных чисел, слов в конечном алфавите N для машины рассматривается последовательность множества В – слова в рамках двоичного кодового алфавита В={0.1}. Также в результат вычисления учитывается «неопределенное» значение, которое возникает при «зависании» алгоритма. Для реализации функции важно наличие формального языка в конечном алфавите и решаемость задачи распознавания корректных описаний.
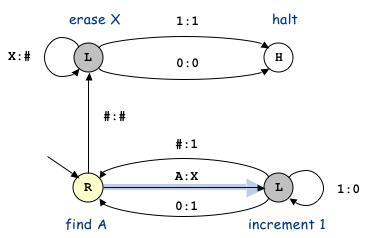
Программа для устройства
Программы для механизма Тьюринга оформляются таблицами, в которых первые строка и столбец содержат символы внешнего алфавита и значения возможных внутренних состояний автомата – внутренний алфавит. Табличные данные являются командами, которые воспринимает машина Тьюринга. Решение задач происходит таким образом: буква, считываемая головкой в ячейке, над которой она в данный момент находится, и внутреннее состояние головки автомата обусловливают, какую из команд необходимо выполнять. Конкретно такая команда находится на пересечении символов внешнего алфавита и внутреннего, находящихся в таблице.

Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Внешний алфавит. Это некоторое конечное множество символов, обозначающихся знаком А, составляющие элементы которого именуются буквами. Один из них – а0 – должен быть пустым. Для примера, алфавит устройства Тьюринга, работающего с двоичными числами, выглядит так: A = {0, 1, а0}.
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Автоматом называется устройство, которое работает без вмешательства людей. В машине Тьюринга он имеет для решения задач несколько различных состояний и при определенно возникающих условиях перемещается из одного положения в другое. Совокупность таких состояний каретки есть внутренний алфавит. Он имеет буквенное обозначение вида Q={q1, q2…}. Одно из таких положений – q1 – должно являться начальным, то есть тем, что запускает программу. Еще одним необходимым элементом является состояние q0, которое является конечным, то есть тем, что завершает программу и переводит устройство в позицию остановки.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
- Запись символа внешнего алфавита в позицию, в том числе и пустого, осуществляя замену находившегося в ней, в том числе и пустого, элемента.
- Перемещение на один шаг-ячейку влево или же вправо.
- Изменение своего внутреннего состояния.
Таким образом, при написании программ для каждой пары символов либо положений необходимо точно описать три параметра: ai – элемент из выбранного алфавита A, направление сдвига каретки (“←” влево, “→” вправо, “точка” — отсутствие перемещения) и qk – новое состояние устройства. К примеру, команда 1 “←” q2 имеет значение “заместить символ на 1, сдвинуть головку каретки влево на один шаг-ячейку и сделать переход в состояние q2”.
Машина Тьюринга: примеры
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 1 | 2 | 3 | … | 7 | 8 | 9 | ||
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | … | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
Пример 2. Дан ряд из символов, обозначающих открывающие и закрывающие скобки. Требуется построить устройство Тьюринга, которое выполняло бы удаление пары взаимных скобок, то есть элементов, расположенных подряд – “( )”. Например, исходные данные: “) ( ( ) ( ( )”, ответ должен быть таким: “) . . . ( (”. Решение: механизм, находясь в q1, анализирует крайний слева элемент в строке.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.
Источник
New Page 1
Для формализации понятия алгоритма была разработана модель, которая названа
машиной Тьюринга (в честь разработчика Алана Тьюринга). Суть этой модели состоит
в том, что существует некий абстрактный исполнитель (абстрактная вычислительная
машина). Этот абстрактный исполнитель является расширением конечного автомата.
Согласно тезису Чёрча — Тьюринга, машина Тьюринга способна имитировать
(при наличии соответствующей программы) любую машину, действие которой
заключается в переходе от одного дискретного состояния к другому.
Под конечным автоматом тут понимают некий абстрактный автомат, имеющий конечное
количество внутренних состояний. Существует множество способов задания конечных
автоматов. Например, конечный автомат может быть графом. Или множеством
M=(V,Q,q0,F,δ),
где
- V — входной алфавит (конечное множество
входных символов), из которого формируются входные слова,
воспринимаемые конечным автоматом; - Q — множество внутренних состояний;
- q0 — начальное состояние
(q Î
Q); F — множество заключительных, или
конечных состояний F Ì
Q;δ —
функция переходов, определенная как отображение
δ : Q
x (V È
{λ})
→ Q,
такое, что
δ(q,a) = {r : q →
a r},
то есть значение функции переходов на упорядоченной паре (состояние, входной
символ или пустая цепочка) есть множество всех состояний, в которые из данного
состояния возможен переход по данному входному символу или пустой цепочке (λ).
Принято считать, что конечный автомат начинает работу в состоянии q0,
последовательно считывая по одному символу входного слова (цепочки входных
символов). Считанный символ переводит автомат в новое состояние, в соответствии
с функцией переходов. Читая входную цепочку символов x и делая переходы
из состояния в состояние, автомат, после прочтения последнего символа входного
слова окажется в некотором состоянии q’. Если это состояние является
заключительным, то говорят, что автомат допустил слово x.
Итак, мы с вами определились, что такое конечный автомат. Машина Тьюринга – это
как раз конечный автомат, точнее, особый вид конечного автомата. Его особенность
заключается в устройстве. В состав машины Тьюринга входит неограниченная в обе
стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных
лент), разделённая на ячейки, и управляющее устройство (также называется
головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества
состояний. Число возможных состояний управляющего устройства конечно и точно
задано. Разумеется, речь идет не о каком то реальной устройстве, а о модели,
виртуальном устройстве.
Управляющее устройство может перемещаться по ленте в обе стороны (влево и
вправо), также оно может читать и писать на лету различные символы определенного
алфавита с конечным числом символов. Выделяется особый пустой символ,
заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых
записаны входные данные. Оно работает согласно правилам перехода, которые
представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое
правило перехода предписывает машине, в зависимости от текущего состояния и
наблюдаемого в текущей клетке символа, записать в эту клетку новый символ,
перейти в новое состояние и переместиться на одну клетку влево или вправо.
Некоторые состояния машины Тьюринга могут быть помечены как терминальные,
и переход в любое из них означает конец работы, то есть, остановку алгоритма.
Есть понятие детерминированной и недетерминированной машины Тьюринга. В первом
случае каждой комбинации считанного с ленты символа и состоянии машины
соответствует однозначное действие: например, переход в другое состояние, запись
конкретного символа на ленту либо смещение ленты в ту или в другую сторону.
Например, если считанный с ленты символ A в состоянии
7 означает запись на ленту символа
B с переходом в состояние 8, то это будет
однозначное действие. Если всем комбинациям состояний и считанных символов
соответствуют подобные однозначные правила, то такая машина Тьюринга и есть
детерминированная.
Но если какой то комбинации символ/состояние соответствует два и более правила,
то это уже будет недетерминированная машина Тьюринга. Например, при считывании
символа X в состоянии 5
происходит либо переход с состояние 6, либо 7. Это уже неоднозначное правило.
Как НМТ «узнаёт», какой из возможных путей приведёт в допускающее состояние?
Есть два пути решения этой проблемы:
- Можно считать, что НМТ — «чрезвычайно удачлива»; то есть всегда выбирает
переход, который в конечном счёте приводит к допускающему состоянию, если
такой переход вообще есть. - Можно представить, что в случае неоднозначности перехода (текущая
комбинация состояния и символа на ленте допускает несколько переходов) НМТ
делится на копии, каждая из которых следует за одним из возможных переходов.
Таким образом, в случае детерминированной машина Тьюринга она имеет некий путь
вычисления, а недетерминированная может иметь дерево вычисления, с
разветвлениями.
Рассмотрим пример. Пусть у нас есть унарная система счисления (в которой только
одна цифра, например, при счете на палочках, как в детстве, когда вас учили
считать). Имеется также машина Тьюринга, которая умножает числа в этой унарной
системе счисления. Имеется правило: «qiaj→qi1aj1R/L/N»,
которое следует понимать так: qi — состояние
при котором выполняется это правило, aj —
данные в ячейке, в которой находится головка, qi1 —
состояние в которое нужно перейти, aj1 — что
нужно записать в ячейку, R/L/N — команда на перемещение.
Набор правил, по которым работает машина, приведены в таблице ниже:
| q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | q01→q01R | q11→q2aR | q21→q21L | q31 → q4aR | q41→q41R | q71→q2aR | |||
| × | q0×→q1×R | q2×→q3×L | q4×→q4×R | q6×→q7×R | q8×→q9×N | ||||
| = | q2=→q2=L | q4=→q4=R | q7=→q8=L | ||||||
| a | q2a→q2aL | q3a→q3aL | q4a→q4aR | q6a→q61R | q7a→q7aR | q8a→q81L | |||
| * | q0*→q0*R | q3*→q6*R | q4*→q51R | ||||||
| q5 →q2*L |
Описание состояний приведены в таблице ниже:
| Начало | |
| q0 | начальное состояние. Ищем «x» справа. При нахождении переходим в состояние q1 |
|---|---|
| q1 | заменяем «1» на «а» и переходим в состояние q2 |
| Переносим все «1» из первого числа в результат | |
| q2 | ищем «х» слева. При нахождении переходим в состояние q3 |
| q3 | ищем «1» слева, заменяем ее на «а» и переходим в состояние q4. В случае если «1» закончились, находим «*» и переходим в состояние q6 |
| q4 | переходим в конец (ищем «*» справа), заменяем «*» на «1» и переходим в состояние q5 |
| q5 | добавляем «*» в конец и переходим в состояние q2 |
| Обрабатываем каждый разряд второго числа | |
| q6 | ищем «х» справа и переходим в состояние q7. Пока ищем заменяем «а» на «1» |
| q7 | ищем «1» или «=» справа при нахождение «1» заменяем его на «а» и переходим в состояние q2 |
| Конец | |
| q8 | ищем «х» слева. При нахождении переходим в состояние q9. Пока ищем заменяем «а» на «1» |
| q9 | терминальное состояние (остановка алгоритма) |
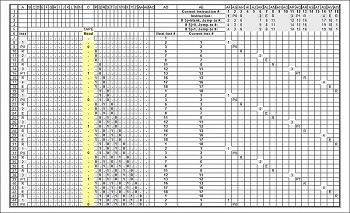
Теперь пояснения к данной таблице. Допустим, нам надо выполнить умножение числа
3 на число 2. В унарной системе это будет 111 и 11 соответственно.
Итак, начло. В машину ввели данные *111×11=*.
Шаг 1. У нас состояние q0
и машина считывает знак “*”. Смотрим по таблице, что она должна делать в этом
случае. Это правило q0*→q0*R
(см. первый столбец, где q0 пятую строку где
*). Это означает, что мы переходим в состояние q0
(то есть, не меняем его). Символ станет “*”, то есть,
также не изменится. Мы смещаемся по введенному нами тексту *111×11=*
вправо на одну позицию (R). В данном случае, это
смещение на первый символ 1.
Шаг 2. Теперь у нас состояние q0
и машина считывает знак “1”. Это означает команду q01→q01R
(см. первый столбец таблицы и первую строку). То есть, снова происходит переход
на одну позицию вправо.
Шаги 3 и 4. Тоже самое, что и на шаге 2. И
тут мы доходим до символа “x”.
Шаг 5. Мы читаем символ
“x”. В состоянии q0
чтение данного символа означает правило q0×→q1×R.
То есть, мы сдвигаемся вправо и переходим в состояние q1.
Шаг 6. Теперь мы уже в состоянии q1
и читаем символ “1”. Это означает правило q11→q2aR.
То есть, мы единичку заменяем на a и сдвигаемся
вправо. Также мы переходим в состояние q2.
Теперь у нас на ленте *111xa1=*
Шаг 7. Мы находимся в состоянии q2,
на ленте у нас *111xa1=*
и мы читаем символ “1”. Это означает правило
q21→q21L.
То есть, мы оставляем в текущей ячейке символ “1”, остаемся в состоянии q2
и сдвигаемся влево. На ленте у нас по прежнему *111xa1=*,
но мы позиционировались на символ “a”, который прочтем
на следующем шаге.
Шаг 8. Находясь в состоянии q2,
мы читаем символ “a”. Такой операции соответствует
правило
q2a→q2aL.
То есть, оставаясь в состоянии q2, мы оставляем в ячейке символ
“a” и сдвигаемся еще левее, туда, где у нас символ
“x”.
Шаг 9. Находясь в состоянии q2,
мы читаем символ “x”. Это соответствует правилу
q2×→q3×L.
Говоря другими словами, мы сдвигаемся на 1 символ влево, переходим в состояние q3
и оставляем в ячейке символ “x”.
Шаг 10. Находясь в состоянии q3,
мы читаем символ “1”. Данной
ситуации соответствует правило
q31 → q4aR.
Выполнение этого правила заменяет на ленте единичку на символ
“a”, теперь у нас на ленте *11axa1=*,
мы перешли в состояние
q4 и сдвигом вправо перешли к ячейке с символом
“x”.
Шаг 11. Находясь в состоянии q4,
мы читаем символ “x”. Данной ситуации соответствие
правило:
q4×→q4×R.
То есть, мы сдвигаемся вправо к следующему символу “a”,
символ “x” остается
неизменным.
Шаг 12. Находясь в состоянии q4,
мы читаем символ “a”. Данной ситуации соответствие
правило:
q4a→q4aR.
То есть, мы сдвигаемся вправо к следующему символу “1”,
символ “a” остается
неизменным.
Шаг 13. Находясь в состоянии q4,
мы читаем символ “1”. Данной ситуации соответствие
правило: q41→q41R.
То есть, мы сдвигаемся вправо к следующему символу “=”,
символ “1” остается неизменным.
Шаг 14. Находясь в состоянии q4,
мы читаем символ “=”. Данной
ситуации соответствие правило: q4=→q4=R.
То есть, мы сдвигаемся вправо к следующему символу “*”,
символ “=” остается
неизменным.
Итак, думаю, как работает машина Тьюринга, из этого примера более менее понятно.
Поэтому далее будут описывать не так подробно.
Итак, в состоянии q4 машина доходит до символа “*” в конце строки и
выполняет правило
q4*→q51R,
которое заменяет “1” и сдвигает указатель вправо. По сути, указатель
позиционируются на пустое место. Но и для этого нас есть правило
q5 →q2*L,
то есть, мы переходим в состояние q2,
ставим к конец слова звездочку и идем обратно (влево). В этом состоянии у нас
машина все идет влево, не меняя символы, пока не наткнется на символ “x”.
тогда она переключается в режим q3,
в котором идет до звездочки, переключается вq6 , согласно
правилу
q3*→q6*R
и начинает обратный ход. У нас на ленте все еще *aaaxa1=111*.
В этом состоянии, чтение символа приведет к выполнению правила
q6a→q61R,
то есть, все звездочки будут заменятся на единички. И так до тех пор, пока не
дойдет до “x”. тогда сработает правило
q6×→q7×R.
То есть, мы переключимся в состояние q7, но
символ “x” пока не тронем. У нас будет на ленте
*111xa1=111*. Далее, в этом состоянии производиться
поиск символа “1”, который, согласно правилу
q71→q2aR,
переключает машину в состояние q2,
а саму единицу заменяет на символ “a”. После этого у
нас будет *111xa1=111*.
Если мы таким же образом отследим манипуляции Машины Тьюринга, то получим
примерно следующее:
| qi | Содержимое памяти |
| q2 | *111xaa=111* |
| q3 | *111xaa=111* |
| q4 | *11axaa=111* |
| q4 | *11axaa=111* |
| q5 | *11axaa=1111 |
| q2 | *11axaa=1111* |
| q3 | *11axaa=1111* |
| q4 | *1aaxaa=1111* |
| q4 | *1aaxaa=1111* |
| q2 | *1aaxaa=11111* |
| q3 | *1aaxaa=11111* |
| q4 | *aaaxaa=11111* |
| q4 | *aaaxaa=11111* |
| q2 | *aaaxaa=111111* |
| q3 | *aaaxaa=111111* |
| q3 | *aaaxaa=111111* |
| q6 | *aaaxaa=111111* |
| q6 | *1aaxaa=111111* |
| q7 | *111xaa=111111* |
| q8 | *111xaa=111111* |
| q8 | *111xaa=111111* |
| q9 | *111×11=111111* |
Машина Тьюринга представляет собой простейшую вычислительную
машину с линейной памятью, которая согласно формальным правилам преобразует
входные данные с помощью последовательности элементарных действий.
Элементарность действий состоит в том, что действие меняет лишь небольшой
кусочек данных в памяти, и число возможных действий конечно. Несмотря на
простоту машины Тьюринга, на ней можно вычислить всё, что можно вычислить на
любой другой машине, осуществляющей вычисления с помощью последовательности
элементарных действий. Это свойство называется полнотой.
Один из естественных способов доказательства того, что
алгоритмы вычисления, которые можно реализовать на одной машине, можно
реализовать и на другой, — это имитация первой машины на второй. Она заключается
в следующем. На вход второй машине подаётся описание программы (правил работы)
первой машины D и входные данные X,
которые должны были поступить на вход первой машины. Нужно описать такую
программу (правила работы второй машины), чтобы в результате вычислений на
выходе оказалось то же самое, что вернула бы первая машина, если бы получила на
вход данные X.
На машине Тьюринга возможно имитировать (с помощью задания
правил перехода) все другие исполнители, каким-либо образом реализующие процесс
пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать любую программу для обычных компьютеров,
преобразующую входные данные в выходные по какому-либо алгоритму. В свою
очередь, на различных абстрактных исполнителях можно имитировать Машину
Тьюринга. Исполнители, для которых это возможно, называются полными по
Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу
машины Тьюринга. Но следует отметить, что данная имитация неполная, так как в
машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с
данными невозможно в полной мере имитировать на компьютере с конечной памятью
(суммарная память компьютера — оперативная память, жёсткие диски, различные
внешние носители данных, регистры и кэш процессора и др. — может быть очень
большой, но, тем не менее, всегда конечна).
В заключении расскажу о таком понятии, как тьюринговская трясина. Этим
сленговым термином обозначают название для языков программирования,
которые Тьюринг-полны, но обладают крайне примитивными синтаксисом и семантикой.
Они неудобны для практического программирования (из-за трудности написания
программ и низкой производительности), зато хорошо подходят для некоторых других
задач (доказательство невычислимости некоторых функций, иллюстрация базовых
принципов программирования и т. д.). Поэтому они интересны для информатики.
Многие эзотерические языки программирования (языки, разработаны для исследования
границ применения некоторой или или просто как шутка) также являются «трясинами
Тьюринга». Пример такого эзотерического языка – язык false,
который выглядит как шифровка, например: “[$1=$[%1]?~[$1-f;!*]?]f:”
(задание функции вычисления факториала).
Источник
